Exercice du maître nageur

Comme promis, voici le problème du maître-nageur :

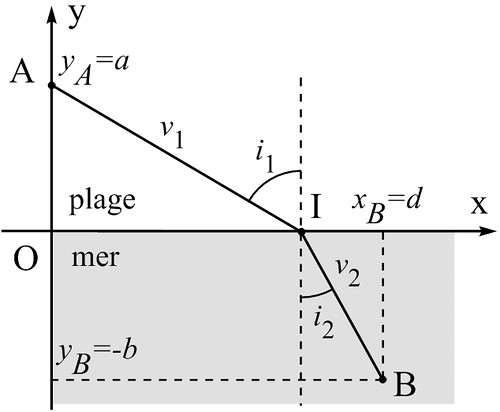
A est sur la plage et B se noie. A peut courir avec la vitesse v₁ et nager avec la vitesse v₂. Il se déplace en ligne droite sur la plage comme dans l'eau. Il atteint l'eau au point I (repéré par l'abscisse x).

1) Quel est la durée t(x) que A met pour atteindre B ?
2) A quelle condition sur x cette durée est-elle extrémale (minimale dans ce cas) ?
3) Montrer que cette condition sur x est équivalente à une relation entre les angles i₁ et i₂.
4) En déduire une analogie avec la loi de la réfraction de Snell-Descartes ainsi que l'énoncé du principe de Fermat.

Une correction existe déjà en ligne, avec des notations similaires, sur le site d'Olivier Granier.
Je vous convie donc à comparer votre réponse avec la sienne : réponse au problème.